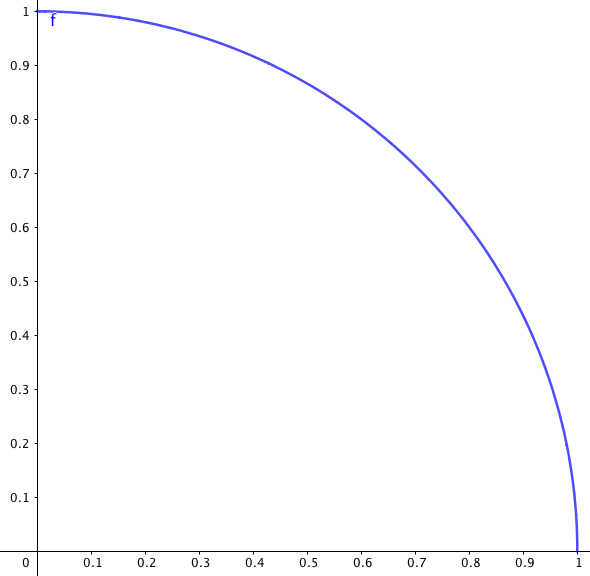
Hvis vi kan sette opp en funksjon som regner ut punkter på en sirkelbue, så kan vi finne punkter med et bestemt mellomrom. La oss ta en kvart sirkel i første kvadrant, som har en radus på 1. Funksjonsuttrykket for denne er:
![]()
På denne måten kan vi finne punkter på buen, finne avstanden mellom punkter (ved hjelp av pytagoras), og legge sammen disse avstandene.

Over ser du hvordan man kan tenke at avstanden mellom to punkter kan regnes ut. x-avstanden er lik hver gang, mens y vil bli ny hver gang.
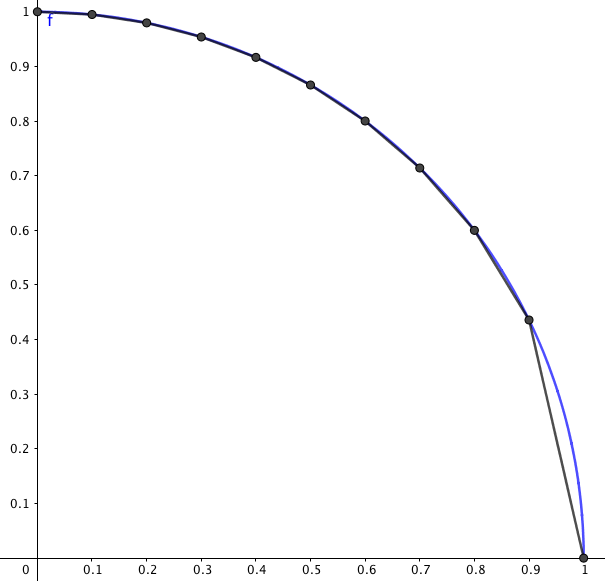
Her vises hvordan det vil bli dersom man bare deler opp 10 ganger. Summen av avstander mellom punkter kommer til å bli litt mindre enn omkretsen av en sirkel, men hvis vi deler den opp i 1000 deler vil den bli mye mer nøyaktig. Kanskje vi kan dele den opp enda mer?
Hva med å benytte cosinus?
Dersom vi deler opp en sirkelsektor i første kvadrant med vinkelhalveringer, så vil vi få mange nye trekanter. La oss se dersom vi deler den opp i 4.
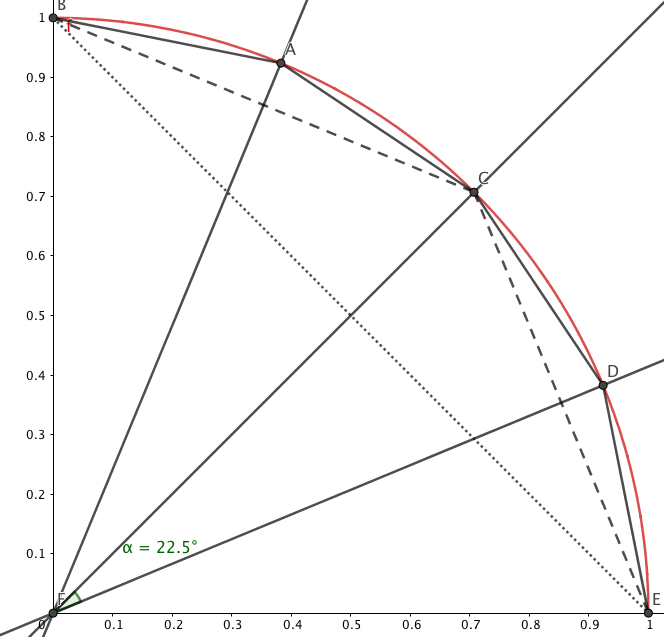
Her ser vi hva som skjer når vi halverer vinkelen flere ganger. Da får vi trekanter som stadig legger seg nærmere sirkelpereferien. Når vi deler opp i 4 like store deler, så vil motstående vinkel bli 22,5 grader. Hvordan kan vi så regne ut motstående side? Jo vi bruker cosinus-setningen og kaller motstående side for s:
![]()
![]()
![]()
Dette er altså avstanden på en slik side. Denne ganger vi med 4 og deretter med 2 for å finne pi, og vårt første overslag blir derfor 3,12. Altså vi nærmer oss allerede pi, bare ved å dele opp figuren vår i 4. Hvor nære kommer vi dersom vi deler opp figuren i …. si 1000?

Legg igjen en kommentar