Idé

La oss se for oss at vi har et kvadrat som er 1×1 meter. I dette kvadratet, så tegner vi en sirkel som tangerer alle sidene. Dersom vi velger et tilfeldig punkt i denne figuren, så må det jo være arealet av sirkelen som avgjør hvor stor sannsynlighet det er for at punktet ligger i sirkelen?
Da er det ingen ting i veien for at vi kan definere et tenkt kvadrat som vi deler opp i….ja, si 1000×1000 og velger tilfeldige punkter ut fra det. Dersom punktet blir 137×945, så må vi sjekke om dette punktet ligger inne i sirkelen.
Hvordan finne ut om punktet ligger i sirkelen?
La oss ta forslaget med et punkt A=(137,945). Hvor vil dette havne i et 1×1 kvadrat? Vel, dersom vi deler opp kvadratet i 1000, så betyr jo det at punktet kommer 0,137 langs førsteaksen og 0,945 langs andreaksen. Hvis vi i tillegg tenker oss at vi plasserer kvadratet i origo, så må både x-verdi og y-verdi ligge mellom -500 og 500. Da kan vi benytte pytagoras til å regne ut avstanden fra sentrum, og dersom den er over 500, så ligger punktet utenfor sirkelen, og dersom punktet er under 500 fra sentrum, så ligger det inne i sirkelen.
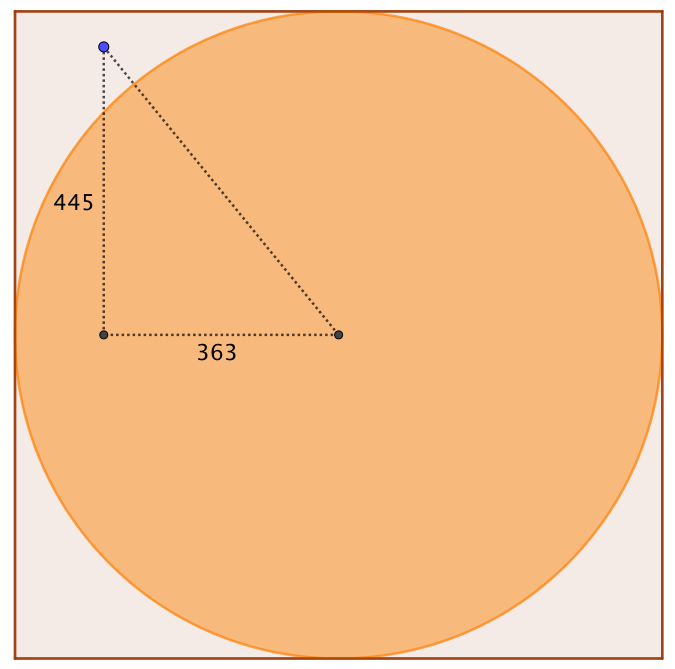
Punktet A vil i en sentrert figur da ligge på A=(-363,445), og avstanden til sentrum regner vi ut slik:
h=sqrt(363^2 + 445^2)
I dette tilfellet, så blir avstanden omtrent 574, så derfor ligger punktet utenfor sirkelen.
Vi kan vel lage et slikt program, som tester ut tilfeldige punkter mange ganger, og sjekker hva sannsynligheten er for at vi «treffer» sirkelen. Finner vi sannsynligheten med mange desimaler, så kan vi jo regne ut pi, med tilsvarende antall desimaler 🙂
Keepin’ it simple!
Trenger vi egentlig å bruke en hel sirkel? Alt vi trenger finnes tross alt i første kvadrant, altså den delen av koordinatsystemet som ligger øverst til høyre, der både x og y verdier er positive. Se figuren nedenfor.
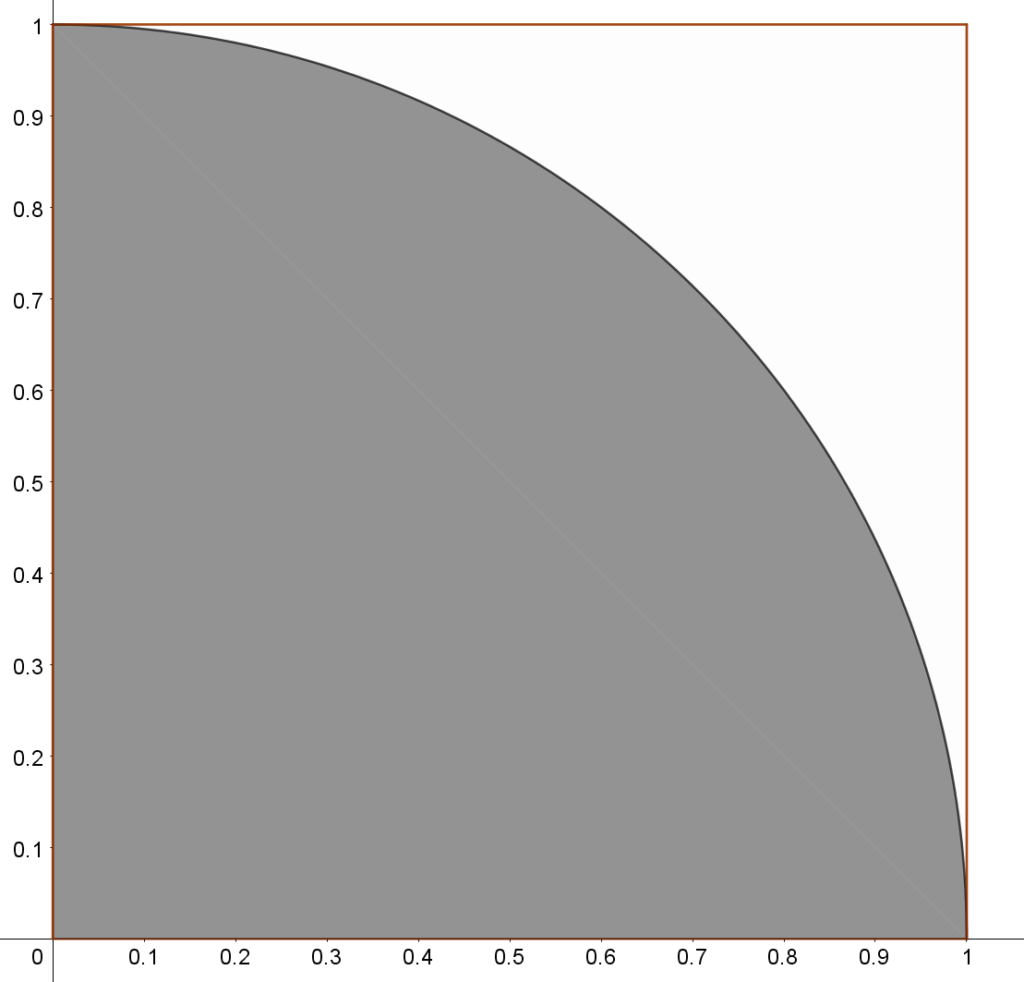
Alt annet er tross alt bare speilinger av denne, så denne bør holde. Hvis vi bruker dette kvadratet til å plukke punkter på, så vil jo sannsynligheten bli det samme her, som i den forrige figuren.
Legg igjen en kommentar